Nick2253
Wizard
- Joined
- Apr 21, 2014
- Messages
- 1,633
Since I haven't seen any discussion on this issue (well, anything more than speculation), I thought I'd go ahead and do some math on exactly what is the likelihood of HDD failure (and, by extension, array failure).
I'll be using the data from Google's HDD study (http://research.google.com/archive/disk_failures.pdf), the Microsoft/U. Virginia study (http://www.cs.virginia.edu/~gurumurthi/papers/acmtos13.pdf), and Microsoft Research (http://arxiv.org/ftp/cs/papers/0701/0701166.pdf). Like any good hard drive manufacturer, 1 TB is 1 trillion bytes.
Now, on to the data.
The annual failure rate (AFR) for the average consumer hard drive (unsegregated by age, temperature, workload, etc), is between approximately 4-6%. The data is corroborated by both the Google and Microsoft studies, as well as other general studies cited in the Microsoft paper. Certain subgroups of hard drives have failure rates below 2%, and certain subgroups have failure rates above 15%.
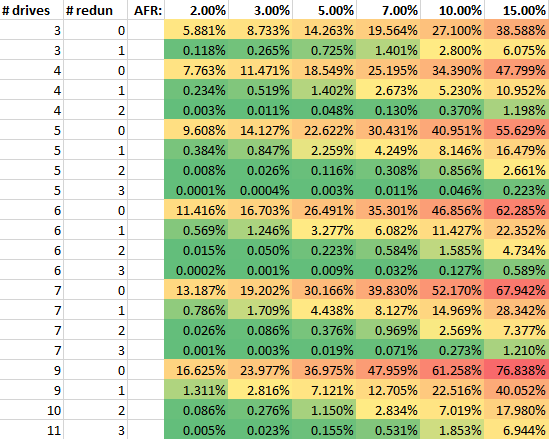
Here's a data table that lists the AFR for an array of "# drives" size with "# redun" redundant disks based on various single-disk AFRs. (For example, a 6 drive RAID10 array would have 6 drives and 3 redundant drives, and if those drives had a 5% AFR, the array would have a 0.009% failure rate).
Array AFR based on number of drives, number of redundant drives, and drive AFR.
What we are calculating here is the likelihood that (# redun + 1) drives or more fails. Mathematically, that looks like (let d = # drives, r = # redun and a = AFR):
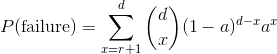
However, disk failures aren't the only cause of array failures. We also have to consider the dreaded unrecoverable read errors (URE), also know as bite error rate (BER).
Now, we've all read cyberjock's article on how RAID5 died in 2009. However, the math in that article isn't quite correct. This is because unrecoverable read errors are not *independent* events. In other words, if you have one URE, you are almost always guaranteed a second one. In a large part, this is driven by the fact that data is not stored in bits on a hard drive, but rather blocks (or sectors).
The causes for URE are diverse, and apart from the internals of the hard drive, include disk controllers, host adapters, cables, electromagnetic noise, etc., so it behooves us to refer to an empirical study on failure rates.
Based on a study by Microsoft in 2005, 1.4 PB of data were read, and only 3 unrecoverable read *events* were recorded. Though each of these events caused multiple bits of data to be lost, only three events occurred.
The table below shows the data for these three theories: that UREs are independent based on manufactures' specifications, that UREs are dependent based on sector failure, and the empirical data from Microsoft.
URE probability for different data read amounts
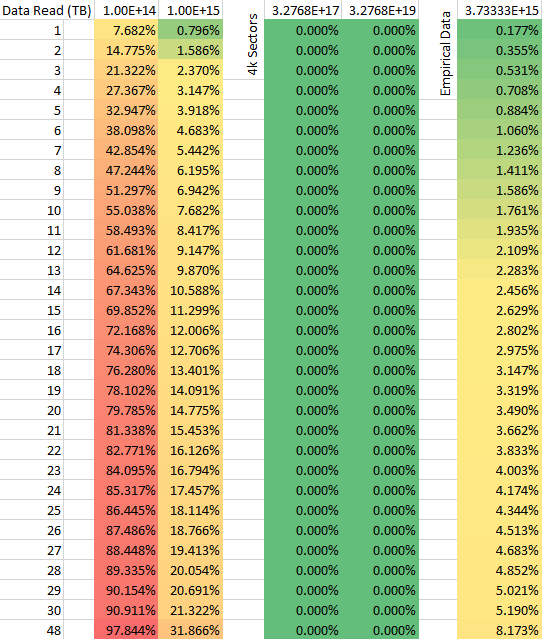
The top row shows bits read per URE (which is the inverse of how it's sometimes reported). What we are calculating here is the likelihood that one or more UREs occurs, or 1-P(no URE). Let s=drive size in bits, U=bits per URE:
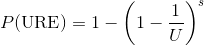
Obviously, UREs cannot be fully independent based on manufacturers' specifications. Anecdotally, during my hard drive burn in, I wrote and read 4 passes of data to my 6 4TB hard drives, which comes to 96TB of data. If UREs were independent, I would have had a 99.95% chance of a URE, yet I did not encounter one.
Also, UREs cannot be dependent based on sectors. Even with 96TB, the likelihood of a URE (under this model) would mean less than one in 1 septillionth of a percent. However, empirically, UREs happen.
Which brings us to the empirical model of 3 failures per 1.4 PB, which translates to a URE rate of 3.73 * 10^15. For my 96TB, this translates to 15.68% likelihood of a URE. Anecdotally, for modern drives, this rate may still overestimate failures, though I have yet to find an empirical study looking for UREs on modern HDDs. Since we're looking for a failure rate, let's be slightly pessimistic and assume that this is in fact the empirical URE rate.
Now, we can combine the HDD failure rate with the URE rate to get a more accurate picture of how protected (or not) our data is.
There are 5 dimensions involved here (drive size, array size, redundant disks, URE rate, and drive AFR), so I've simplified some of the dimensions for usability. Using the methods here, you should be able to calculate your array failure rate if your parameters.
Array AFR based on various factors
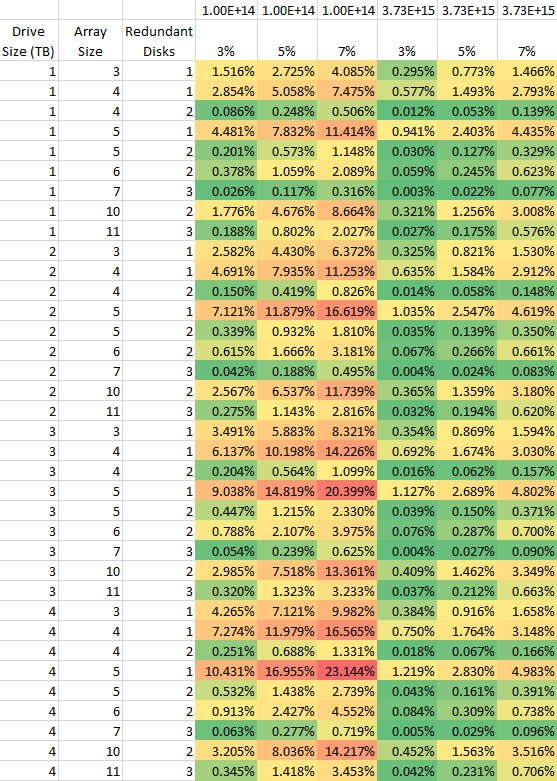
Across the top is the URE rate in bits per URE and the next row is AFR for the individual hard drive. Mathematically, I'm calculating:
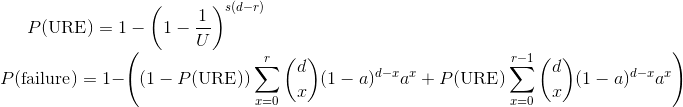
The equation above can simplify quite a bit, but I left it in this form because it is more intuitive. What we have is the same P(URE) from before, and our new P(failure) is 1-P(success), which is the probability that we don't have a URE and we have 0 to r drive failures, and the probability that we have a URE and we have 0 to r-1 drive failures.
Results
What we find is that, even under our empirical URE rate, RAID5/RAIDZ1 arrays are still incredibly risky. AFR for these arrays can be as bad as 5%.
It's also important to note that drive AFR is very important for array AFR. Decreasing your drive AFR by a small amount (e.g. better cooling, minimizing vibration, replacing older drives) pays back in large dividends. For example, decreasing the AFR from 7% to 3% on a six drive RAIDZ2 array decreases the AFR for the array by 10x.
I hope this has been educational for you all. If you have any other questions, let me know.
I'll be using the data from Google's HDD study (http://research.google.com/archive/disk_failures.pdf), the Microsoft/U. Virginia study (http://www.cs.virginia.edu/~gurumurthi/papers/acmtos13.pdf), and Microsoft Research (http://arxiv.org/ftp/cs/papers/0701/0701166.pdf). Like any good hard drive manufacturer, 1 TB is 1 trillion bytes.
Now, on to the data.
The annual failure rate (AFR) for the average consumer hard drive (unsegregated by age, temperature, workload, etc), is between approximately 4-6%. The data is corroborated by both the Google and Microsoft studies, as well as other general studies cited in the Microsoft paper. Certain subgroups of hard drives have failure rates below 2%, and certain subgroups have failure rates above 15%.
Here's a data table that lists the AFR for an array of "# drives" size with "# redun" redundant disks based on various single-disk AFRs. (For example, a 6 drive RAID10 array would have 6 drives and 3 redundant drives, and if those drives had a 5% AFR, the array would have a 0.009% failure rate).
Array AFR based on number of drives, number of redundant drives, and drive AFR.
What we are calculating here is the likelihood that (# redun + 1) drives or more fails. Mathematically, that looks like (let d = # drives, r = # redun and a = AFR):
However, disk failures aren't the only cause of array failures. We also have to consider the dreaded unrecoverable read errors (URE), also know as bite error rate (BER).
Now, we've all read cyberjock's article on how RAID5 died in 2009. However, the math in that article isn't quite correct. This is because unrecoverable read errors are not *independent* events. In other words, if you have one URE, you are almost always guaranteed a second one. In a large part, this is driven by the fact that data is not stored in bits on a hard drive, but rather blocks (or sectors).
The causes for URE are diverse, and apart from the internals of the hard drive, include disk controllers, host adapters, cables, electromagnetic noise, etc., so it behooves us to refer to an empirical study on failure rates.
Based on a study by Microsoft in 2005, 1.4 PB of data were read, and only 3 unrecoverable read *events* were recorded. Though each of these events caused multiple bits of data to be lost, only three events occurred.
The table below shows the data for these three theories: that UREs are independent based on manufactures' specifications, that UREs are dependent based on sector failure, and the empirical data from Microsoft.
URE probability for different data read amounts
The top row shows bits read per URE (which is the inverse of how it's sometimes reported). What we are calculating here is the likelihood that one or more UREs occurs, or 1-P(no URE). Let s=drive size in bits, U=bits per URE:
Obviously, UREs cannot be fully independent based on manufacturers' specifications. Anecdotally, during my hard drive burn in, I wrote and read 4 passes of data to my 6 4TB hard drives, which comes to 96TB of data. If UREs were independent, I would have had a 99.95% chance of a URE, yet I did not encounter one.
Also, UREs cannot be dependent based on sectors. Even with 96TB, the likelihood of a URE (under this model) would mean less than one in 1 septillionth of a percent. However, empirically, UREs happen.
Which brings us to the empirical model of 3 failures per 1.4 PB, which translates to a URE rate of 3.73 * 10^15. For my 96TB, this translates to 15.68% likelihood of a URE. Anecdotally, for modern drives, this rate may still overestimate failures, though I have yet to find an empirical study looking for UREs on modern HDDs. Since we're looking for a failure rate, let's be slightly pessimistic and assume that this is in fact the empirical URE rate.
Now, we can combine the HDD failure rate with the URE rate to get a more accurate picture of how protected (or not) our data is.
There are 5 dimensions involved here (drive size, array size, redundant disks, URE rate, and drive AFR), so I've simplified some of the dimensions for usability. Using the methods here, you should be able to calculate your array failure rate if your parameters.
Array AFR based on various factors
Across the top is the URE rate in bits per URE and the next row is AFR for the individual hard drive. Mathematically, I'm calculating:
The equation above can simplify quite a bit, but I left it in this form because it is more intuitive. What we have is the same P(URE) from before, and our new P(failure) is 1-P(success), which is the probability that we don't have a URE and we have 0 to r drive failures, and the probability that we have a URE and we have 0 to r-1 drive failures.
Results
What we find is that, even under our empirical URE rate, RAID5/RAIDZ1 arrays are still incredibly risky. AFR for these arrays can be as bad as 5%.
It's also important to note that drive AFR is very important for array AFR. Decreasing your drive AFR by a small amount (e.g. better cooling, minimizing vibration, replacing older drives) pays back in large dividends. For example, decreasing the AFR from 7% to 3% on a six drive RAIDZ2 array decreases the AFR for the array by 10x.
I hope this has been educational for you all. If you have any other questions, let me know.
