ChrisReeve
Explorer
- Joined
- Feb 21, 2019
- Messages
- 91
First of all, all hardware specs are in my signature.
Long story short, I had a server crash, and after a reboot, two drives were out of sync. I possibly could have synced them again (not sure if this is possible), but I decided to just resilver them one at a time.
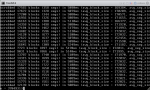
While resilvering the first one, it slowed down to a halt (original resilver time was 2-3 days, but after slow down, it kept increasing to 40-50 days and icreasing), indicating an issue. I tried to do a smart check on the drive I was resilvering, and it wasnt responding. I decided to reboot freenas, which worked fine, but it seems like it started an automatick full scrub on restart. This seems to be trucking on without issues, but I am unable to access freenas in the browser, and I am unable to type anything in the command line interface (direct access, see screenshot).
I assume I should just let it finish. It seems to be progressing nicely, and the stability issues were most likely due to insufficient cooling. We were going through a period of extreme heat when the server crashed, and I have no Air Conditioning.
The question. Does it seem normal (SEE SCREENSHOT), and can I estimate a completeion time based on the reported speed, and size of pool?
Pool: 10x10TB WD Red White Label drives, single vdev RAIDz2. Total raw space 90TiB, total usable space, 67TiB.
According to the screenshot, the reported speed seems to be around 2 800 000 000 to 3 700 000 000 (bits/bytes?). I am uncertain of the unit that is reported, but I believe it is bytes.
Assuming avg_seg_size is reported in bytes, and assuming an average scrub speed of 3 000 000 000 bytes per 5 seconds:
This gives me 600 000 000 Bytes/second, or 572MB/s scrub speed. Does that seem realistic for my setup?
Also, assuming 572MB/s, and a total raw space of about 90TB, should I expect the scrubbing process to take about 165 000 seconds, or 45 hours.
Are my assumptions correct?
Long story short, I had a server crash, and after a reboot, two drives were out of sync. I possibly could have synced them again (not sure if this is possible), but I decided to just resilver them one at a time.
While resilvering the first one, it slowed down to a halt (original resilver time was 2-3 days, but after slow down, it kept increasing to 40-50 days and icreasing), indicating an issue. I tried to do a smart check on the drive I was resilvering, and it wasnt responding. I decided to reboot freenas, which worked fine, but it seems like it started an automatick full scrub on restart. This seems to be trucking on without issues, but I am unable to access freenas in the browser, and I am unable to type anything in the command line interface (direct access, see screenshot).
I assume I should just let it finish. It seems to be progressing nicely, and the stability issues were most likely due to insufficient cooling. We were going through a period of extreme heat when the server crashed, and I have no Air Conditioning.
The question. Does it seem normal (SEE SCREENSHOT), and can I estimate a completeion time based on the reported speed, and size of pool?
Pool: 10x10TB WD Red White Label drives, single vdev RAIDz2. Total raw space 90TiB, total usable space, 67TiB.
According to the screenshot, the reported speed seems to be around 2 800 000 000 to 3 700 000 000 (bits/bytes?). I am uncertain of the unit that is reported, but I believe it is bytes.
Assuming avg_seg_size is reported in bytes, and assuming an average scrub speed of 3 000 000 000 bytes per 5 seconds:
This gives me 600 000 000 Bytes/second, or 572MB/s scrub speed. Does that seem realistic for my setup?
Also, assuming 572MB/s, and a total raw space of about 90TB, should I expect the scrubbing process to take about 165 000 seconds, or 45 hours.
Are my assumptions correct?